Лекція 5-6
Перетворення схем Янова
КРАТКОЕ ПОВТОРЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
§ 6.1. Логические формулы и булевы функции
Предмет логики. Логика, подобно арифметике и геометрии, является одной из математических дисциплин, с предметом которой человек, даже того не ведая, имеет дело с первых лет своей сознательной жизни. Более правильным было бы, пожалуй, сказать, что законы правильного рассуждения о предметах и явлениях, наряду со свойствами форм предметов и количественными соотношениями между предметами, являются главным содержанием: математики, если говорить о ее вкладе в повседневную человеческую практику. Интересно, однако, отметить, что логика, будучи как организующий элемент человеческого общения много старше математики, стала сама объектом математического изучения совсем недавно: по-настоящему лишь в конце девятнадцатого века. Это тем более парадоксально, что математическая логика в чем-то проще многих других^ разделов математики. Этому парадоксу есть свое объяснение, которое, однако, автор не может изложить здесь с должной глубиной. Мы заметим только, что, с одной стороны, математики в течение долгого времени и при этом в целом успешно полагались на здравый смысл в применении законов логического рассуждения, пока конкретный математический материал (обоснование математического анализа, парадоксу теории множеств, неевклидова геометрия) не подвели их к необходимости заняться логическими основами самой математики. С другой стороны, необходимо было достичь высокого уровня абстрактного мышления и своего рода доверия к символике, чтобы правильно найти исходные абстракции логических рассуждений и быть уверенным в универсальной применимости формально выведенных законов логики, выраженных в символической форме.
В этой повторительной главе мы дадим краткий обзор одного из разделов математической логики — алгебры логики и исчисления высказываний, который, по мнению автора, обладает многими замечательными качествами. Объекты этой теории и относящиеся к ней задачи сравнительно просты; в то же время доказываемые в алгебре логики и исчислении высказываний свойства и теоремы глубоки и содержательны, применимы к многим явлениям реального мира и многое в нем объясняют. Построение теории, будучи весьма стройным и естественным, одновременно содержит в себе, как в зародыше, общую структуру многих богатых и сложных теорий современной математики.
Одна из целей логического рассуждения — это установление истины, т. е. возможности достоверно подтвердить или опровергнуть некоторое высказывание. Уже в одной этой фразе содержатся одновременно некоторое наблюдение и некоторое ограничение. Человек рассуждает, произнося фразы на человеческом, или, как говорят, естественном языке. Ограничение состоит в том, что мы рассматриваем лишь такие фразы естественного языка (высказывания), о которых имеет смысл говорить, что они правильны или неправильны, истинны или ложны. Наблюдение подсказывает нам, что свойства истинности или ложности оказываются взаимно дополняющими; другими словами, естественный язык устроен так, что если мы имеем некоторое ложное высказывание («Москва — столица Франции»), то всегда можно высказать его отрицание, являющееся истинным высказыванием («Неверно, что Москва — столица Франции»), и наоборот. При этом такой переход от утверждения к его отрицанию можно осуществить" простой перестройкой фразы, не вникая в ее смысл (с этой точки зрения переход от ложного высказывания «Москва — столица Франции» к истинному — «Париж — столица Франции» или «Москва — столица СССР» — это не то правило перехода от утверждения к его отрицанию с помощью приставки «неверно, что...», а содержательная подмена одного высказывания другим, выполняемая за рамками формальных законов логики.
Анализируя высказывания, образующие цепочку логического рассуждения, мы обнаруживаем в нем то, что обычно называется исходными фактами, т. е. самыми простыми суждениями, истинность или ложность которых установлена заранее, или, более точно, средствами, находящимися за рамками данного логического рассуждения. Правила естественного языка позволяют из исходных фактов составлять более сложные производные высказывания. При этом, как и в случае правила отрицания, мы усматриваем, что существуют такие правила построения сложных высказываний, в которых свойство высказывания быть истинным или ложным зависит только от истинности или ложности составляющих исходных фактов и от того, каким образом они комбинируются в сложное высказывание. В естественном языке эти правила выглядят как сочленение высказываний с помощью следующих выделенных слов:
НЕВЕРНО, ЧТО (НЕВЕРНО, ЧТО Москва — столица Франции) — отрицание;
И (шел дождь И шли два студента) — конъюнкция;
ИЛИ (он пьет ИЛИ он курит) — дизъюнкция;ВЛЕЧЕТ (преступление ВЛЕЧЕТ наказание, бузина в
огороде ВЛЕЧЕТ дядьку в Киеве, свист рака ВЛЕЧЕТ молоко от козла, 2x2 = 4
ВЛЕЧЕТ, что Волга впадает в Каспийское море, но НЕВЕРНО, ЧТО истина ВЛЕЧЕТ
ложь) — импликация;
ИЛИ . . . ИЛИ (ИЛИ он украл пальто, ИЛИ у него укради пальто) — альтернатива;
ТО ЖЕ, ЧТО (х простое число — ТО ЖЕ, ЧТО х делится только на себя и единицу) — тождество.
Мы позволили себе привести в качестве примеров несколько расхожих выражений, чтобы резче подчеркнуть, что можно точно говорить об истинности или ложности сложных высказываний, даже не задумываясь об их содержательном значении, если только правила понимания указанных союзов и оборотов (называемых логическими связками) раз и навсегда оговорены.
Эти правила употребления становятся, как обычно, особенно четкими, если их представить в символической форме, в которой исходные факты будут изображаться как независимые логические переменные, принимающие два значения I (ложь) и I (истина), а логические связки — как логические операции с двумя аргументами:
х & у - конъюнкция (другое обозначение: х /\ у;
х \/ у — дизъюнкция;
х 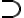 у — импликация (другое
обозначение: х-± у;
у — импликация (другое
обозначение: х-± у;
х называется посылкой, а у —
заключением импликации);
x + y — альтернатива;
х ≡ у — тождество;
и как операция над одним аргументом:
~]х — отрицание (другое обозначение: х).
Значениями логических операций являются те же два значения f и t. Таким образом эти операции полностью описываются таблицами своих значений, называемыми таблицами истинности
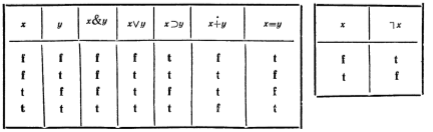
Глядя на эти таблицы истинности и на задающие их логические связки, можно
сделать следующее наблюдение: если сложное высказывание осмысленно, то его
смысл не противоречит значению истинности, полученному по правилам вычисления
логических операций. Именно это наблюдение (не теорема!) дает нам основание
верить в полезность далее развиваемой теории.
Логические формулы. Итак, мы осуществляем первый этап построения теории, вводящий некоторую символику для конструирования логических формул.
Логические формулы строятся из символов:
f, t — логические константы (значения истинности), .
A, B, С, . . ., X, У, Z — логические переменные,
( , ) — скобки,
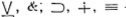 — двуместные логические
операции,'
— двуместные логические
операции,'
 — одноместная
логическая операция {в дальнейшем для краткости будем слово «логический» иногда
спускать).
— одноместная
логическая операция {в дальнейшем для краткости будем слово «логический» иногда
спускать).
Константа или переменная — это первичная формула.
Если Ф — формула, то (Ф) — первичная формула.
Если Ф — первичная формула, то Ф — одночлен.
Если Ф — одночлен, то  Ф — одночлен.
Ф — одночлен.
Если Ф — одночлен, то Ф — конъюнкция.
Если Ф1 — конъюнкция, а Ф2 — одночлен, то Ф1& Ф2—конъюнкция.
Если Ф — конъюнкция, то Ф — дизъюнкция.
Если Ф1 — дизъюнкция, а Ф2 — конъюнкция, то Ф1\/ Ф2 или
Ф1 + Ф2 — дизъюнкции.
Если Ф — дизъюнкция, то Ф — импликация.
Если Фх — импликация и Ф2 — дизъюнкция, то Ф1 Ф2 — импликация.
Если Ф — импликация, то Ф — формула.
Если Ф1 — формула иФ2- импликация, то Ф1 ≡ Ф2 — формула.
Других формул нет.
Эти педантичные определения хороши тем, что они дают совершенно точное определение логических формул, устанавливая одновременно правила старшинства в выполнении логических операций. На языке школьной алгебры можно сказать, что раньше всего выполняются действия в скобках, потом — в порядке перечисления — отрицание конъюнкция
дизъюнкция и альтернатива
импликация
тождество.
Автор надеется, что этой апелляции к опыту читателя будет достаточно, чтобы удостовериться, что, например, такой текст
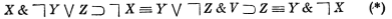
является правильной формулой, в котором выделение аргументов для каждой операции происходит единственным образом, а именно
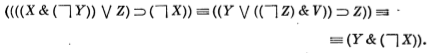
Формальный синтаксис. Здесь нам будет уместно несколько отвлечься от основной нити изложения. Дело в том, что только что данное индуктивное определение логических формул основано на общем приеме, которой настолько важен в программировании, что не поговорить о нем, имея подходящий повод, было бы непростительно.
Сначала заметим, что для таких индуктивных конструкций применяется простая символика, позволяющая сделать определение более компактным и наглядным. Общий смысл индуктивного определения состоял в том, что мы последовательно определяли все более и более широкие классы формул, начиная с «первичных формул», через «одночлены», «конъюнкции», «дизъюнкции» и «импликации» — к общему понятию «формулы». Кроме этого, мы вводили промежуточные буквенные обозначения Ф, Ф1, Ф2, чтобы показать, как конкретно конструируется тот или иной класс формул. Первое правило символики, которую мы сейчас вводим, позволяет вместо буквенных обозначений использовать сами названия строящихся конструкций, заключенные для определенности в угловые скобки. Это позволит вместо фразы
«если Ф1 — импликация и Ф2
— дизъюнкция, то Ф1 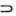 Ф2 — импликация»
Ф2 — импликация»
писать короче
<импликация>:: = <импликация> 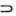 <дизъюнкция> где
знак : : = означает «равно по определению». Эта запись, равно как и исходное
словесное определение, означает способ задания множества формул, называемых
«импликациями» через множество «импликаций» же и множество «дизъюнкций»
следующим образом. Надо взять любую «импликацию», приписать к ней знак
<дизъюнкция> где
знак : : = означает «равно по определению». Эта запись, равно как и исходное
словесное определение, означает способ задания множества формул, называемых
«импликациями» через множество «импликаций» же и множество «дизъюнкций»
следующим образом. Надо взять любую «импликацию», приписать к ней знак 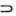 , за которым поместить любую «дизъюнкции;». Полученная строчка
текста по определению является элементом множества «импликаций». Заметим, что в
нашей системе правил нет никакого заколдованного круга, так как для начального
множества импликаций есть другое определение, которое гласит «если Ф — дизъюнкция,
то Ф — импликация» или — в новой символике —<импликация> :: = <дизъюнкция>.
, за которым поместить любую «дизъюнкции;». Полученная строчка
текста по определению является элементом множества «импликаций». Заметим, что в
нашей системе правил нет никакого заколдованного круга, так как для начального
множества импликаций есть другое определение, которое гласит «если Ф — дизъюнкция,
то Ф — импликация» или — в новой символике —<импликация> :: = <дизъюнкция>.
Таким образом для импликации мы имеем два альтернативных определения, которые объединяются вместе с использованием
13 А. П, Ершов вертикальной черты, отделяющей в правой части конструкции одну альтернативу от другой:
<импликация> :: = <дизъюнкция> |<импликация> <дизъюнкция>
Сама конструкция называется металингвистической формулой, а определяемые конструкции — металингвистическими переменными (имея в виду, что их значениями являются элементы конструируемого множества допустимых объектов, в данном случае — логических формул).
Все правила для логических формул целиком выглядят следующим образом:
(константа) :: = f | t
(переменная) :: = А\В\С . . . \X\Y\Z
(первичное) :: = <константа> |<переменная> |(<формула>)
(одночлен) :: = <первичное> | <одночлен>
<одночлен>
(конъюнкция)
:: = <одночлен> | <конъюнкция>& <одночлен> (дизъюнкция) ::
= <конъюнкция>|<дизъюнкция> \/ <конъюнкция>
<конъюнкция>& <одночлен> (дизъюнкция) ::
= <конъюнкция>|<дизъюнкция> \/ <конъюнкция>
|<дизъюнкция> + (конъюнкция)
(импликация)
:: = (дизъюнкция) | (импликация) 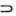 (дизъюнкция)
(дизъюнкция)
(формула) :: = (импликация)[(формула) ≡ (импликация).
В такой трактовке правила задания формул напоминают грамматику естественного языка, в которой роль частей речи играют металингвистические переменные. Это сходство не случайно, и в математике часто называют языком любой регулярный способ задания конструктивных объектов, образующих некоторое множество L слов в заданном алфавите. Более точно, языком называют само множество L, а способ задания языка L называют его формальной грамматикой.
Строгое описание формальной грамматики само требует некоторой символики, описываемой обычно в каком-то другом языке, называемом метаязыком, используемым для описания языка L. В нашем случае мы описываем язык логических формул, используя метаязык металингвистических формул. Список металингвистических формул называют синтаксисом описываемого языка.
Понятие формальной грамматики в применении к естественным языкам сложилось наиболее полно в 50-е годы в работах американского лингвиста и математика Н. Хомского. Аппарат металингвистических формул был в 1959 г. предложен американским математиком и программистом Дж. Бэкусом и использован его датским коллегой П. Науром в 1960 г. для описания языка алгол 60. В их честь грамматики, описанные с помощью металингвистических формул, называют БНФ-грамматиками (бэкусово- наурова форма). С тех нор этот аппарат широко применяется для описания языков программирования, а в последние годы перекочевывает и в чисто математические работы.
Уточнение способа описания логических формул позволяет нам теперь более точно сказать, что значит, что «выделение аргументов для каждой операции происходит единственным образом».
Пусть нам дана какая-то логическая формула. По правилам БНФ-грамматики мы усматриваем, что она или оказывается импликацией, или строится из другой логической формулы, знака операции = и некоторой импликации. Читатель может проверить, что выбор альтернативы в этом анализе будет производиться однозначно. Эта однозначность является важным свойством удачно составленной БНФ-грамматики. Итак, для каждой логической формулы мы можем построить один из двух таких графов:
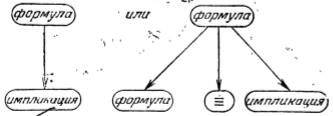
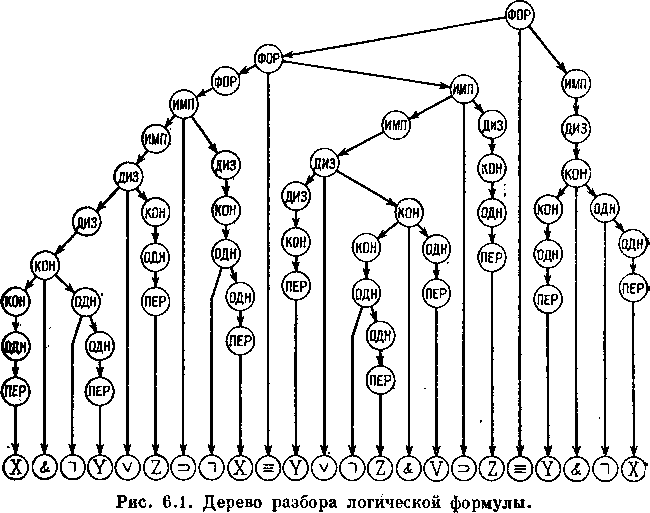
При этом мы не только единственным образом выбираем альтернативу, но и однозначно разбиваем текст исходной формулы на части, сопоставляемые нижним металингвистическим переменным. Это означает, что для каждой из выделенных, как говорят, «прямых конституент» исходной формулы мы можем в свою очередь однозначно выбрать составляющие их подформулы, нарастив наш граф снизу еще одним слоем металингвистических переменных или символов исходного алфавита. Этот процесс «разбора» формулы будет продолжаться, пока по каждому направлению в строящемся графе (он, очевидно, окажется деревом) мы не доберемся до символа исходного алфавита, который станет терминалом дерева. Полученный граф, который оказался построенным однозначно для взятой логической формулы, называется ее деревом разбора. Его вершинами яляются символы исходного алфавита и металингвистические переменные. Для краткости и общности первые называются терминальными, а вторые — нетерминальными символами БНФ-грамматики. |
Дерево разбора для приведенной логической формулы (*) показано на рис. 6.1. .
Булевы
функции. Здесь уместно вспомнить, ради чего был разведен этот формализм.
Мы ввели логические формулы как средство точного описания сложных высказываний
(логических формул),, истинность которых может быть установлена на основе
истинности исходных фактов (логических переменных) с использованием 13*
+++содержательных свойств логических связок
(логических операций), виданных своими таблицами истинности.
Для того чтобы оправдать наш язык логических формул, мы должны теперь дать им должную интерпретацию, т. е. показать, как получить суждение об истинности или ложности логической формулы, если нам известны значения истинности исходных фактов (логических переменных формулы).
С использованием дерева разбора «момент истины» достигается с помощью следующей индуктивной процедуры.
Базис индукции: терминальным символам — переменным (логическим константам) заданы (присущи) некоторые значения истинности.
Шаги индукции: если нетерминальный символ n имеет единственную конституенту с приписанным ей значением истинности о, то а приписывается символу n;
если нетерминальный символ n
является одночленом вида
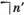 и
и
символу n'
приписано значение 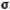 , том получает значение
, том получает значение 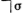 (по таблице
истинности);
(по таблице
истинности);
если нетерминальный символ
м является конструкцией вида 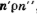 ,
,